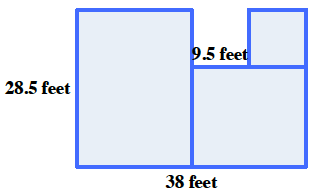
Home > CC1 > Chapter 8 > Lesson 8.1.5 > Problem 8-69
8-69.
Draw a figure that is made of rectangles and has a perimeter of
Remember that the perimeter is the distance around a shape and the area is the space within the shape.
Below is one example of a figure with a perimeter of 152 feet. Can you draw a different figure?