
Home > CCA2 > Chapter 3 > Lesson 3.2.1 > Problem 3-63
3-63.
Given that
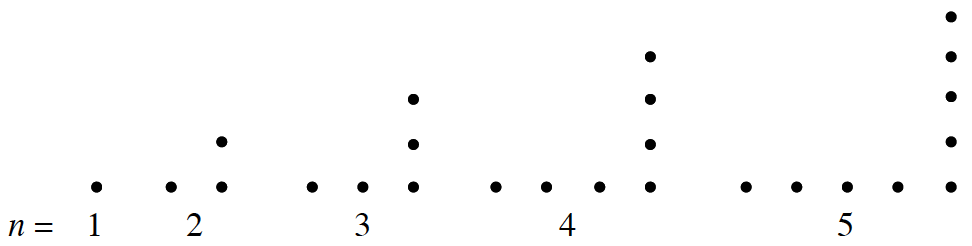
Find a rule for the sequence. How does the figure number relate to parts in the shape?
n | |
|---|---|
t(n) |
Look at the two legs. One way to see figure 3, for example, is a row of 3 and a column of 2 above it (note: you can't count the dot in the corner twice). How would you analyze figure 4 in the same way?
Now use the idea to analyze the
The
The