Home > CCA2 > Chapter 4 > Lesson 4.2.1 > Problem 4-76
Multiply or divide the rational expressions below. Write each answer in simplified form.
Multiply across the numerator and denominator.
Look for factors that simplify to one.
Convert the quotient to a product.
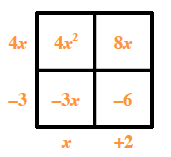
Use a generic rectangle to factor each trinomial. 2 by 2 square
Put the first and last terms in opposite corners. Added to square interior, top left, 4, x, squared, bottom right, negative 6.
The products of the diagonals need to be equal. In this case find two (missing) terms whose product is
. For this expression their sum must be . Write the missing terms in the blank corners of the rectangle.Added interiors, top right, 8, x, bottom left, negative 3, x.
Find the greatest common factor of each row and column. Write the factors on the outside of the rectangle. Added to left edge, top, 4, x, bottom, negative 3. Added to bottom edge, left, x, right, + 2.
The side 'lengths' of the rectangle are the factors of the trinomial.
You can use this method to factor the other three trinomials. Then, complete the division problem. If you need more help, see problem 3-78 (c).