In parts (a) through (d) below, for each polynomial function $f(x)$, the graph of $f(x)$ is shown. Based on this information, state the number of linear and quadratic factors the factored form of its equation should have and how many real and complex (non-real) solutions $f(x)= 0$ might have. (Assume a polynomial function of the lowest possible degree for each one.)

Example: $f(x)$ at right will have three linear factors, therefore three real roots and no complex roots. 

1. 

   Answer (a):

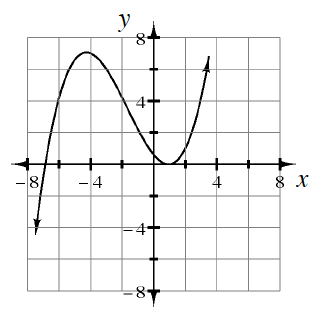
   There will be three linear factors (one repeated), therefore two real (one single, one double) and zero complex (non-real) roots.

2. 

   Answer (b):

   There will be one linear factor and one quadratic factor, therefore one real and two complex (non-real) roots.

3. 

   Answer (c):

   There will be four linear factors, therefore four real and zero complex (non-real) roots.

4. 

   Answer (d):

   There will be two linear and one quadratic factor, therefore two real and two complex (non-real) roots.