CPM Homework Help : CCA2 Problem 8-120

Carlos is always playing games with his graphing calculator, but now his calculator has contracted a virus. The $\boxed{\text{TRACE}}$ , $\boxed{\text{ZOOM}}$ , and $\boxed{\text{WINDOW}}$ functions on his calculator are not working. He needs to solve
$x^3 + 5x^2 - 16x - 14 = 0$ , so he graphs $y = x^3 + 5x^2 - 16x - 14$ and sees the graph at right in the standard window.

3 lines, 2 appear almost vertical, while middle one is decreasing. The lines cross the x axis, as follows: Left line, at negative 7. Middle line, between negative 1 & 0. Right line, between 2 & 3.

From the graph, what appears to be an integer solution to the equation?
Answer (a):
$x = -7$
Check your answers from part (a) in the equation.
Hint (b):
Substitute your answer from part (a) into the original equation.
Since $x=-7$ is a solution to the question, what is the factor associated with this solution?
Answer (c):
$(x + 7)$
Use polynomial division to find the other factor.
Step 1(d):
Divide $x^³ + 5x^² − 16x − 14$ by $x + 7$
using a generic rectangle. 2 by 3 rectangle, labeled as follows: left edge, x, & 7, top edge left, x squared, interior top left, x cubed.
Step 2(d):
Labels added to the rectangle, interior top middle, negative 2, x squared, interior bottom left, 7, x squared.
Step 3(d):
Labels added to rectangle, top edge, middle, negative 2, x, interior, bottom middle, negative 14, x, interior top left, negative 2, x.
Answer (d):
Labels added to rectangle, top edge, right, negative 2, interior bottom right, negative 14.
$x^2 - 2x - 2$

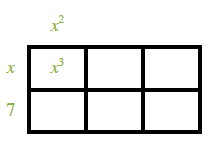
Use your new factor to complete this equation:
$x^3 + 5x^2 - 16x - 14 =$ ( $x+7$ )(other factor) $=0$
The “other factor” leads to two other solutions to the equation. Find these two new solutions and give all three solutions to the original equation.
Hint (f):
Use the Quadratic Formula with the answer found in part (d) that you used for part (e).