
Home > CCA2 > Chapter 8 > Lesson 8.3.1 > Problem 8-121
Now Carlos needs to solve
If
So divide
2 by 3 rectangle, labeled as follows: left edge, x, minus 1, interior top left, 2, x cubed, bottom expression: 2, x cubed, + 3, x squared, minus 8, x, + 3. An arrow points from the interior 2, x cubed to the bottom, 2, x cubed.
Label added: top edge, left, 2, x squared.
Label added: interior bottom, left, negative 2, x squared.
Label added: interior top middle, 5, x squared, with arrow, going through, interior bottom left, negative 2, x squared, ending, in the bottom expression, at 3, x squared.
Label added, top edge, middle, 5, x.
Label added, Interior bottom, middle, negative 5, x.
Label added, interior top, right, negative 3, x, with arrow, going through, interior bottom, middle, negative 5, x, ending, in the bottom expression, at negative 8, x.
Label added, top edge, right, negative 3.
Label added, interior bottom, right, 3.
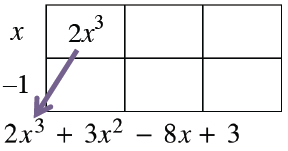






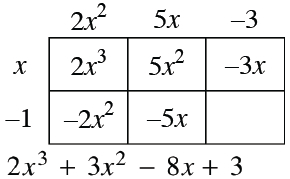

Write the equation in factored form.
Factor the quadratic expression and use the Zero Product Property to obtain the three solutions.