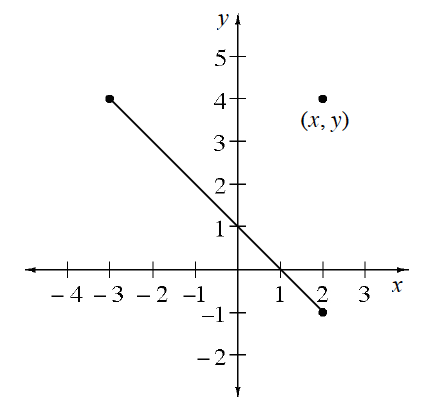Home > CCA2 > Chapter C > Lesson C.1.1 > Problem C-9
C-9.
In the diagram at right, the point
What is the distance from
to ? Do you remember the equation to determine the distance between two points?
What is the distance from
to ? Use the same equation as in part (a).
Write the equation that states that the two expressions in (a) and (b) are equal and simplify.
Set your two distance equations from parts (a) and (b) equal to each other.
Then simplify this larger equation until it is inform. What is the specific name of the geometric object represented by your equation from part (c)?
Try graphing your answer from part (c).
How does this new graph relate to the original line?