
Home > CCG > Chapter 10 > Lesson 10.1.4 > Problem 10-46
10-46.
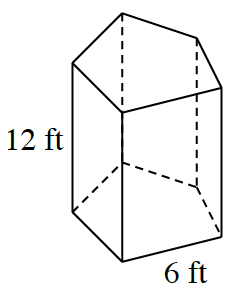
Find the central angle of the pentagon.
The area of the triangle will help you find the area of the pentagon.
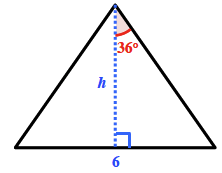
Find the area of each of the sides, and sum them to find the surface area.
Multiply the area of the pentagon by the height to find the volume.