
Home > CCG > Chapter 10 > Lesson 10.1.5 > Problem 10-54
10-54.
In the diagram at right,
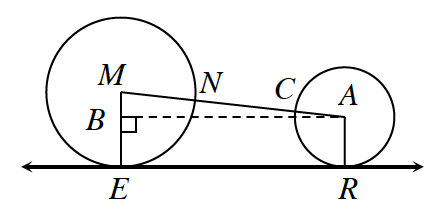
Think about how the radius of
How will the radius of
After finding the lengths of
Use Pythagorean Theorem to find the length of the last side.

In the diagram at right,

Think about how the radius of
How will the radius of
After finding the lengths of
Use Pythagorean Theorem to find the length of the last side.