
Home > CCG > Chapter 9 > Lesson 9.1.3 > Problem 9-34
9-34.
A regular hexagonal prism has a volume of
Start by finding the area of the base of the prism

Divide the hexagon into six triangles.
Find

Divide the triangles in half to make two right triangles.
Solve for unknown angles. Is this a special triangle?
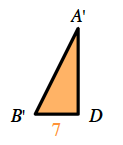
When you find the area of the
Once you have the height of the prism, you have all the information necessary to find the surface area.