Home > APCALC > Chapter 2 > Lesson 2.2.1 > Problem 2-52
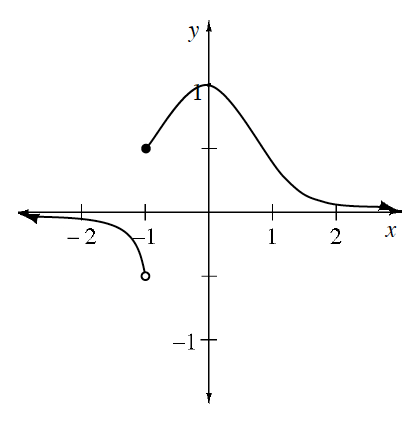
Write as many limit statements as you can about the function graphed at right as
Limits give information about the location of holes and asymptotes, because they are predicted values, not real values.
An Intuitive Definition of Limit
When you graph a function
For example, if
You can also take one-sided limits using numbers less than
An important point is that