A horizontal flag is shown at right. The radius of the outer semicircle is $4$. The radius of the inner semicircle is $3$.

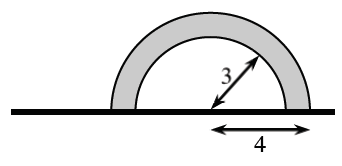
1. Imagine rotating the flag about its pole and describe the resulting three-dimensional figure. Sketch this figure on your paper.

   Hint (a):

   Imagine a hollow rubber ball. The rubber is $1$-inch thick and the radius is $3$ inches.

2. Calculate the volume of the rotated flag.

   Hint (b):

   $\text{Volume} = \text{big sphere} − \text{small sphere}$

   Answer (b):

   $\frac{4}{3}\pi(4)^3-\frac{4}{3}\pi(3)^3=\frac{148}{3}\pi \text{ un}^{3}$