The graph of $x^3 = 5xy + 2y^2$ is shown below.  

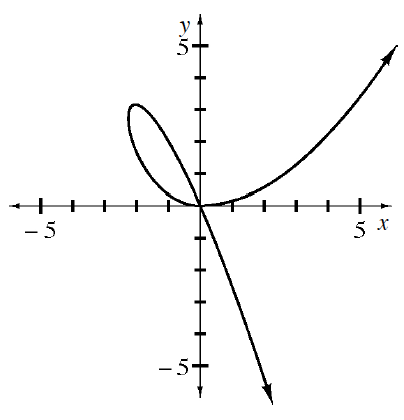
1. How many tangent lines exist at $x = -2$?

   Hint (a):

   How many coordinate points does this graph have at
   $x = −2$?

2. Write the equations of the tangent lines at $x = -2$.

   Hint (b):

   Write two tangent line equations in point-slope form.
   You already know the points.

   Hint (b):

   Use the derivative to find the corresponding slopes. You will have to use implicit differentiation.

   Hint (b):

   Because you used implicit differentiation, your derivative might have both $x$- and $y$-values.
   That means you will need $\left(x, y\right)$ coordinate points to evaluate.