Home > CALC > Chapter 12 > Lesson 12.2.2 > Problem 12-80
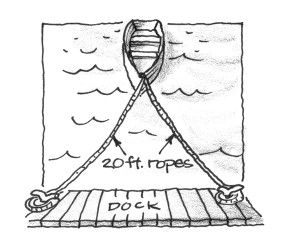
A rowboat is tethered to a long dock by two ropes, each 20 feet long. Both ropes from the bow of the rowboat are tied to the dock at points 20 feet apart. The two ropes and the section of dock between them form an equilateral triangle.
The boat's owner unties one of the ropes from the dock, and brings the boat toward the dock by walking along it away from the other rope at a rate of 4 feet per second. How fast is the boat moving toward the dock when the man has walked 10 ft.? Homework Help ✎
Draw a diagram where the d = distance from the dock, which is the height of an isosceles triangle.
Let x = distance the owner has walked.
When the owner has walked 10 ft, by the Pythagorean Theorem, d = √ 175 .
Substitute in the known values and solve for d′.