The rate of customers who pass through the checkout stand at a grocery store depends on the time of day. Assume the rate follows the following piecewise function, where $x$ represents the time of day (in hours) after 9:00 a.m. and $f\left(x\right)$ is the number of customers served per hour.

$f ( x ) = \left\{ \begin{array} { l l } { 120 x } & { \text { for } 0 \leq x < 2 } \\ { 180 x - 120 } & { \text { for } 2 \leq x < 5 } \\ { 240 x - 420 } & { \text { for } x \geq 5 } \end{array} \right.$

1. Graph the function and name its domain and range.

   Graph (a):

   Your sketch should have three linear pieces.

   Hint (a):

   The domain is given by the piecewise function above.

   More Help (a):

   The range can be seen on the graph. What is the highest and lowest y-value? Are there any holes or jumps on that interval?

   

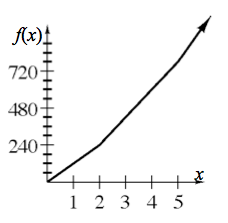
2. Is this function continuous?

   Hint (b):

   We know that the graph has a starting point $\left(0,0\right)$ so, it could only be continuous when $x>0$.

   More Help (b):

   Be mindful of the 3 conditions of continuity:

   

3. Find $A\left(f, 0 ≤ x ≤ 8\right)$. What are the units of this area? What does this area represent?

   Hint (c):

   $\text{Area} = k\left(\text{base}\right)\left(\text{height}\right)$, where $k$ is some constant. The base is determined by the units on the $x$-axis. The height is determined by the units on the $y$-axis. Multiply.