CPM Homework Help : CALC Problem 2-140

WHICH IS BETTER? Part Three

Below is a comparison of using a different number of rectangles to approximate the same area under a curve for $f(x)$ . Decide which will best approximate $A(f, a ≤ x ≤ b)$ . Explain why.

If, in each situation, the rectangles all had equal widths, write expressions to find the area under the curve.

Hint:

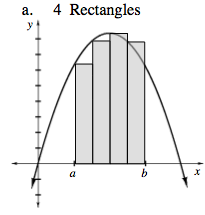
Look at the shaded area beneath each curve. Which sketch most accurately represents the actual area under the curve?

More Help:

General form for left-endpoint Riemann sum using sigma notation:

Answer (a):

$\displaystyle\sum_{i=0}^{3}\frac{b-a}{4}f\left ( a+\frac{b-a}{4}i \right )$

Answer (b):

$\displaystyle\sum_{i=0}^{9}\frac{b-a}{10}f\left ( a+\frac{b-a}{10}i \right )$

Answer (c):

$\displaystyle\sum_{i=0}^{19}\frac{b-a}{20}f\left ( a+\frac{b-a}{20}i \right )$