Home > CALC > Chapter 3 > Lesson 3.1.1 > Problem 3-11
Below is the graph of the function f(x) = 2x3 with tangents drawn at x = −2, −1, 1, and 2. Use the slopes provided in the graph to find the slope function f ′(x). Notice that f ′(0) = 0. It might be helpful to make a table of data relating x to m. Homework Help ✎
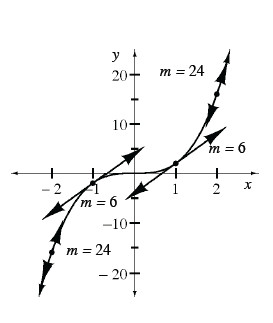
The data in the table was taken from the graph.
'x' represents x-values.
'm ' represents slope of the tangent line.
The original graph, f(x), is cubic. Does the table of slopes also appear to have a cubic pattern? If not, what type of function would model its pattern?
The slopes have a quadratic pattern! Clearly, the data does not fit the parent quadratic equation: y = x2. Find a transformation of y = x2 that models the data.
Use the eTool below to view the tangent lines.
Click on the link to the right to view the full version of the eTool: Slope at a Point eTool