Midpoint rectangles have their height defined at the midpoint of the interval. For the function $f ( x ) = \frac { 1 } { 2 } x + \operatorname {cos}(x)$ graphed below, you previously found the heights to be $f(1.5) ≈ 0.821$, $f(2.5) ≈ 0.449$, $f(3.5) ≈ 0.814$.

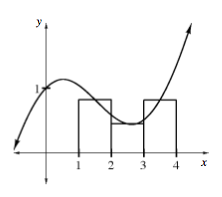
1. Approximate $A(f, 1 ≤ x ≤ 4)$ using midpoint rectangles.

   Hint 1(a):

   There are only three rectangles.
   No need to use sigma notation.

   Hint 2(a):

   Just find the area of each rectangle and add. Be sure to organize your work in a way that others will understand your process.

2. Find the exact area and compare it with your approximation.

   Hint (b):

   Find the exact area using a definite integral.