CPM Homework Help : CALC Problem 8-95

Multiple Choice: The function $f(x) = x^2$ is bounded by the y-axis and the line $y = 4$ . The volume generated by revolving the region about the $y$ -axis can be found by which of the following integrals?

$2 \pi \int _ { 0 } ^ { 2 } x ( 4 - x ^ { 2 } ) d x$

$\pi \int _ { 0 } ^ { 4 } y d y$

$\pi \int _ { 0 } ^ { 4 } \sqrt { y } d y$

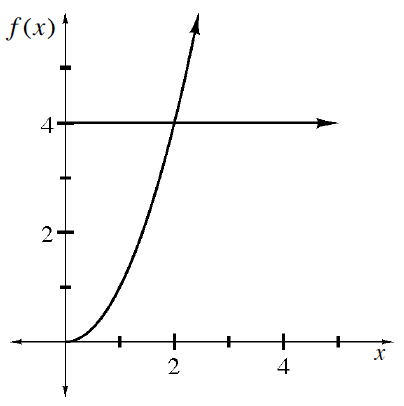
I only

II only

III only

I and II

I and III

Hint:

If you want to use disks/washers, then rotate horizontal rectangles...
that means that both the bounds and the integrand must be written in terms of $y$ .

$\text{Disks: }\pi \int_{y=a}^{y=b}(f(y))^{2}dy$

$\text{Washers: }\pi \int_{y=a}^{y=b}(f(y))^{2}-(g(y))^{2}dy$

If you want to use shells, then use $x$ -values.