CPM Homework Help : CALC Problem 8-142

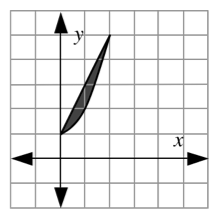
The region M is enclosed by the functions $f(x) = x^2 + 1$ and $g(x) = 2x + 1$ . Set-up, but do not evaluate, the integrals to represent the volumes of the solids formed by revolving M about each of the following axes.

Graph:

The $x$ -axis.
Hint (a):
Sketch the axis of rotation (flag pole) then use washers.
$V=\pi \int_{x=a}^{x=b}(R)^{2}-(r)^{2}dx$

The $y$ -axis.
Hint (b):
Use shells.
$V=2\pi \int_{x=a}^{x=b}xf(x)dx$
Note the $x$ represents the length of the radius, it's part of the base $= 2πr$ equation. And $f(x)$ represents the height of each shell.

The line $y = 5$ .
Hint 1(c):
Refer to the hint in part (a).
Hint 2(c):
Recall that R and r represent radii of an outer and inner solid (the 'inner' solid is the hole). Make R the function with the longer radii and r the function with the shorter radii. Note: It is possible that R is below r on the graph. Once rotation happens, this will switch.
Hint 3(c):
Also note that both radii have different lengths than $f(x)$ and $g(x)$ , since the axis of rotation is $5$ units above the $x$ -axis. Adjust the integral in part (a) accordingly:
$V=\pi \int_{x=a}^{x=b}(k-R)^{2}-(k-r)^{2}dx$

The line $x = 4$ .
Hint 1(d):
As in part (b), to avoid using horizontal rectangles (and rewriting the integrand in terms of $y$ ), you can use shells.
Hint 2(d):
The setup should look exactly like the setup in part (b), with one exception: The radii are no longer the same values as the bounds. They will be either longer or shorter than the bounds. So shift the radii $k$ units to the left or right:
$V=2\pi \int_{x=a}^{x=b}(x-k)f(x)dx$