CPM Homework Help : INT2 Problem 7-10

What else can you prove about parallelograms? Prove that the diagonals of a parallelogram bisect each other. For example, assuming that quadrilateral $WXYZ$ at right is a parallelogram, prove that $\overline{WM} ≅ \overline{YM}$ and $\overline{ZM} ≅ \overline{XM}$ . Fill in the missing statements and reasons in the flowchart proof below. Then record your theorem in your Theorem Graphic Organizer.

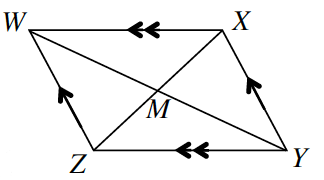
Parallelogram W, X, Y, Z with two diagonals inside intersecting at point M. Side W, Z and side X ,Y are each marked with one arrow. Side W, X and side Z, Y are each marked with two marks.

Flow chart outline with 8 ovals: 1 flows to 2 & 5, 3, 4, 5 flow to 6, 6 flows to 7 & 8. All ovals blank except the following: #3 if lines are parallel, alternate interior angles are congruent. #5: Opposite sides of a parallelogram are congruent. #7: Segment, WM, congruent to segment, YM. #8 Segment, ZM, congruent to segment, XM.

Hint:

Start by proving $ΔXWM ≅ ΔZYM$ by ASA $≅$ . Think about parallel lines and angles while working on this proof.

More Help:

What reason justifies that $\overline{WM} ≅ \overline{YM}$ and $\overline{ZM} ≅ \overline{XM}$ ?

Flow chart outline with 8 ovals: 1 flows to 2 & 5, 3, 4, 5 flow to 6, 6 flows to 7 & 8. Outside #3: if lines are parallel, alternate interior angles are congruent. Outside #5: Opposite sides of a parallelogram are congruent. Inside #7: Segment, W,M, congruent to segment, Y,M. Inside #8 Segment, Z,M, congruent to segment, X,M.