CPM Homework Help : INT3 Problem 2-30

Maura is deciding which hose to use to water her outdoor plants. Maura notices that the water coming out of her garden hoses follows a parabolic path.

When Maura uses her green garden hose the greatest height the water reaches is $8$ feet, and it lands on the plants $10$ feet from where she is standing. Both the nozzle of the hose and the top of the flowers are $4$ feet above the ground.

Maura has already determined that when she has the water on full blast, the water from the red hose follows the path $y=-(x-3)^2+7$ .

Hint:

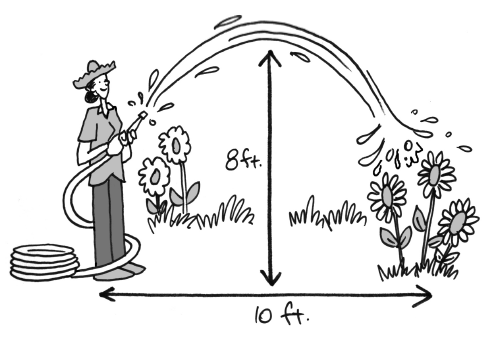
The domain is all the possible $x$ -values that make sense in this problem. The range is all the possible $y$ -values that make sense in the problem. For example, there won’t be any negative $y$ -values here.

Which hose will throw the water higher?
Write an equation that models the path of the water from Maura’s green hose.
What domain and range make sense for the water from Maura’s green hose?

Use the eTool below to check your work.
Click the link at right for the full version of the eTool: Int3 2-30 HW eTool