When you stack one function machine on top of another so that the output of the first machine becomes the input of the second machine, you create a new function, which is a composition of the two functions. If the first function is $f(x)$ and the second is $g(x)$, the composition of the functions can be written as the composite function $g(f(x))$.

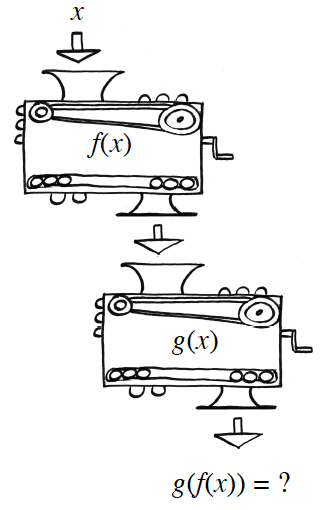
1. The function machines $f(x) = x^2 - 1$ and $g(x) = 3(x + 2)$ are stacked as shown at right. If $x$ is input at the top, what expression comes out of the bottom? That is, what is the composite function $g(f(x))$?

   Hint (a):

   This is $g(x^2 − 1)$.

   Answer (a):

   $g(f(x))=3((x^{2}-1)+2)$

2. Write an expression for the composite function $f(g(x))$.

   Answer (b):

   $f(g(x))=(3(x+2))^{2}-1$