CPM Homework Banner

Home > INT3 > Chapter 8 > Lesson 8.3.1 > Problem 8-102

8-102.

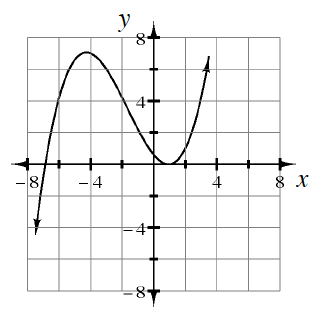
Each graph below represents a polynomial function. For each function, state its minimum degree. Then state the number of real and complex roots it has.

Example: The graph of at right has degree . It has three real roots and no complex roots.

  1. A curved continuous graph, with arrows at both ends, that rises from the bottom left, to the approximate point, (negative 4.5, comma 7), then falls to the approximate point, (1 half, comma 0), then rises again.

    Degree
    There are two distinct real roots, one of which is repeated.

  1. A curved continuous graph, with arrows at both ends, that rises from the bottom left, to the point, (negative 4, comma 6), then falls to the approximate point, (1, comma 3), then rises again.

  1. Continuous, curved graph, decreasing from top left, turning at the following approximate points: low vertices: (negative 4, comma negative 7), & (3, comma negative 1), & high vertex, (0, comma 1.5), with x intercepts, at negative 6, negative 1, 2, & 4..

  1. Continuous, curved graph, decreasing from top left, turning at the following approximate points: low vertices: (negative 2, comma 2), & (5, comma negative 2), & high vertex, (1, comma 4), with x intercepts, at 3, & 5.5.

    Degree
    There are two real roots and two complex roots.

A curved continuous graph, with arrows at both ends, that rises from the bottom left, to the approximate point, (negative 4.5, comma 2), then falls to the approximate point, (1 half, comma negative 2), then rises again.

© 2022 CPM Educational Program. All rights reserved.