CPM Homework Help : INT3 Problem 9-101

The CPM Amusement Park has decided to imitate The Screamer but wants to make their ride even better. Their ride will consist of a circular track with a radius of $100$ feet, and the center of the circle will be $50$ feet under ground. Passengers will board at the highest point, so they will begin with a blood-curdling drop. Write a function that relates the angle traveled from the starting point to the height of the rider above or below the ground.

Step 1:

Begin by sketching a unit circle to model the situation. When the passenger boards at $90^\circ$ on the unit circle (but $0^\circ$ traveled), they are $50$ feet above ground.

When they have traveled $90^\circ \left(\frac{\pi}{2}\text{ radians}\right)$ the passenger has moved to $50$ feet below ground, or the center point.

After traveling $180^\circ(\pi \text{ radians})$ they are $150$ feet below ground.

After moving $270^\circ \left(\frac{\pi}{2} \text{ radians}\right)$ , they are back to $50$ feet below ground.

They return to $50$ feet above ground after turning a full circle, $360^\circ(2\pi \text{ radians})$ .

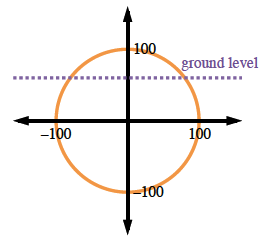
Circle centered at the origin, with dashed horizontal line, at y = 50, labeled, ground level. Labels at the intersections of the circle with the axes labeled as follows: positive x axis, 100, positive y axis, 100, negative x axis, negative 100, negative y axis, negative 100.

Step 2:

Make a table of values then sketch the graph.

x (radians)	y (feet)
$0$	$50$
$\frac{\pi}{2}$	$-50$
${\pi}$	$-150$
$\frac{3\pi}{2}$	$-50$
$2{\pi}$	$50$
$\frac{5\pi}{2}$

Step 3:

Determine the parameters of the equation.
As with any periodic function, either $y = \sin x$ or $y = \cos x$ could be the parent graph for the equation.
Since we have started at a high point, we will use cosine as the parent.
Determine the horizontal and vertical shifts and the amplitude.

Step 4:

The horizontal shift $\left(h\right)\ \text{is}\ 0$ . The vertical shift (k) is $50$ feet down. The amplitude (a) is $100$ .
Substitute the parameters into the general equation, $y = a · \sin\left(x − h\right) + k$ .
Use a graphing calculator to see that your equation matches your graph.

Answer:

$y = 100\text{sin} \left(x + \frac{\pi}{2}\right) - 50\text{ or }y = 100 \text{cos}(x) - 50$