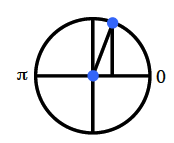
Many times when we are solving trigonometric equations, the solutions are not convenient values on the unit circle where we can find the exact answers. For example, when we solve $2 \sin x = 1$, we get $x = \sin^{−1}( \frac { 1 } { 2 } )$ and we know the exact solution between $-\frac { \pi } { 2 }$ and $\frac { \pi } { 2 }$ is $\frac { \pi } { 6 }$. The other solution between $0$ and $2π$ is $\frac { 5 \pi } { 6 }$. But what happens when we try to solve $5 \sin x = 4$?

1. Solve $5 \sin x = 4$ for $x$ and calculate a decimal approximation.

   Step (a):

   $\sin (x) =\frac { 4 } { 5 }$

2. Is this the only solution between $0$ and $2π$? Use what you know about the symmetry of the sine wave to determine the other solution between $0$ and $2π$ to this trigonometric equation.

   Hint (b):

   Use the unit circle and symmetry.

   Where else is the $\sin x=\frac{4}{5}$?

   How can you write this?

   

   Answer (b):

   $x = 0.927$
   $x = π − 0.927$

3. Using the same method, find all of the solutions for the domain $\left(−∞, ∞\right)$.

   Hint (c):

   Add $2πn$ where $n =$ any integer to both answers above.