CPM Homework Help : PC Problem 9-114

A rectangular corral is to be built using $900$ ft of fencing. Three sides will need fencing. The fourth side will border a river. The goal is to make a rectangular corral that has the maximum possible area under these conditions.

Sketch the situation.
Answer (a):
Write an equation for the area of the corral as a function of $x$ , the length of the side perpendicular to the river.
Answer (b):
$2x + y = 900$
$y = 900 − 2x$
Area $= \left(x\right)\left(900 − 2x\right)$

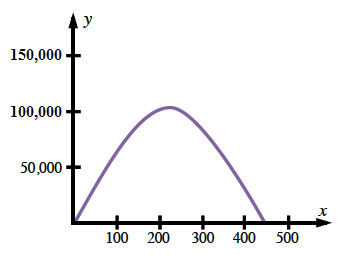
Graph this function.
Graph (c):
first quadrant Downward parabola, turning at (225, comma 101,250), x-intercepts at 0 & 450.
Which value of $x$ gives you the maximum area?
Answer (d):
Coordinates at turning point added, (225, comma 101,250)
What is the slope of the tangent line to the area graph at this point?
Answer (e):
Slope of the tangent line is $0$ .