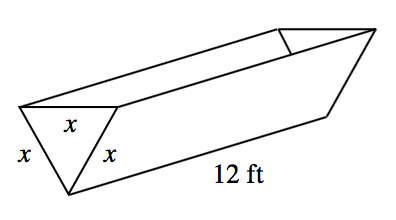
A trough is in the shape of an equilateral triangular prism, as shown in the diagram at right. The length of the trough is $12$ feet.  

1. Write an equation for the height of the equilateral triangle in terms of $x$.

   Hint (a):

   Draw and label the triangle with information you know. Use the Pythagorean Theorem to solve for the height.

   Answer (a):

   $\frac{\sqrt{3}}{2}x$

   

2. Write an equation for the volume $V$ of the trough in terms of $x$.

   Hint (b):

   $V(x)=$ (area of the triangle)(length of the trough)

3. If the trough can hold $200\text{ ft}^3$ of water, how deep is the trough?

   Hint (c):

   Solve $200=V(x)$.