
Home > A2C > Chapter 6 > Lesson 6.2.5 > Problem 6-118
Consider two functions
Use these two functions to write an equation for a composite function and sketch its graph.
A composition of two functions is when the output of the first function becomes the input of the second.
or 
Use these two functions to write a different composite function and sketch its graph.
See part (a).
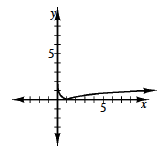
What makes the two composite functions so different from each other?
Remember that the order of composition matters.
When using the absolute value first, you can use both positive and negative numbers for x, so the domain is different from the domain for the log function.When using the log first and then taking the absolute value, only positive values can be used for x. If the result of the log is negative, the absolute value makes it positive, so the range is only positive numbers.
Challenge: Now try graphing
. Think this through; you can do it!

Use the eTool below to view the graph of the equations and solve the parts of the problem.
Click the link at right for the full version of the eTool: 6-118 HW eTool