Home > A2C > Chapter 8 > Lesson 8.1.5 > Problem 8-85
8-85.
Sketch a graph of

Is it a function?
Does each x-value on the graph of the function have only one corresponding y-value?
What are its domain and range?
Domain: −10 ≤ x ≤ 10
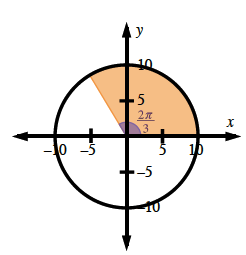
Range: −10 ≤ y ≤ 10Draw a central angle that measures
radians. If you remove this wedge of the circle, how much area remains? See the unit circle graph at right.
What portion of the circle is shaded?