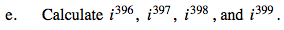Consider this geometric sequence: i⁰, i¹, i², i³, i⁴, i⁵ , …, i¹⁵.

1. You know that i⁰ = 1, i¹ = i, and i² = −1. Calculate the result for each term up to i¹⁵, and describe the pattern.

   Hint (a):

   i⁰ = 1 Can you see the pattern?

   i¹ = i

   i² = −1

   i³ = (i)(i²) = −i

   i⁴ = (i²)(i²) = 1

   i⁵ = (i²)(i²)(i) = i

   Answer (a):

   The pattern repeats 1, i, −1, and −i

2. Use the pattern you found in part (a) to calculate i¹⁶, i²⁵, i³⁹, and i¹⁰⁰.

   Hint (b):

   16 is a multiple of 4.
   25 is on more than a multiple of 4.
   39 is one less than a multiple of 4.
   100 is a multiple of 4.

   Answer (b):

   i¹⁶ = 1
   i²⁵ = i
   i³⁹ = −i
   i¹⁰⁰ = 1

3. What is i⁴ⁿ , where n is a positive whole number?

   Hint (c):

   4n is a multiple of 4.

4. Based on your answer to part (c), simplify i⁴ⁿ⁺¹, i⁴ⁿ⁺², and i⁴ⁿ⁺³.

   Hint (d):

   Refer to (a), (b), and (c).

5. Calculate i³⁹⁶, i³⁹⁷, i³⁹⁸, and i³⁹⁹.

   Hint (e):

   i³⁹⁶ = i^4·99 = 1

   i³⁹⁷ = i^4·99+1 = ?

   i³⁹⁸ = i^4·99+2 = ?

   i³⁹⁹ = ?