CPM Homework Help : GC Problem 11-75

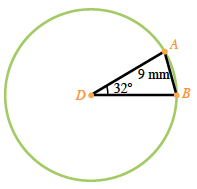
The length of chord $\overline{AB}$ in $⊙D$ is $9$ mm. If the $m\overarc{ A B }=32º$ , find the length of $\overarc{ A B }$ . Draw a diagram.

Step 1:

Draw a diagram and label with all known values.

Hint:

Use $ΔABD$ to find the length of the circle's radius. Then calculate the circumference of the entire circle ( $2rπ$ ) and find the length of the arc as a fraction of the whole circle.

More Help:

$\triangle ABD$ is isosceles. $\overline{AD} \cong \overline{BD}$ because both are radii.

Step 2:

Find the measures of the other two angles:
Find the length of the radius either by using the Law of Sines, or by dividing the triangle into two equal right triangles and using trigonometry ratios.

$m\angle DAB = m\angle DBA$

$m\angle ADB + m\angle DBA + m\angle DAB = 180º$

$m\angle ADB = 32º$ , then $m\angle DBA$ and $m\angle DAB = 74º$

Method 1:

Using the Law of Sines:

$\frac{\sin32º}{9} = \frac {\sin74º}{r}$

$(\frac{\sin32º}{9} = \frac {\sin74º}{r})9r$

$r \cdot \sin32º = 9 \cdot \sin74º$

$r = \frac{9 \cdot \sin74º}{\sin32º} \approx 16.33$

Method 2:

Using right triangles:

$\sin16º = \frac{4.5}{r}$

$r \cdot \sin 16º = 4.5$

$r = \frac{4.5}{\sin16º} \approx 16.33$

Circle, with center, D, points, A, &, B, line segments from, D, to, A, from D, to, B, from, A, to, B, angle, A, D, B, labeled 32 degrees, chord, A, B, labeled 9 mm.

A circle with the center, D, and two points on the circumference, A & B. The triangle A, B, D has a central angle at D, 32 degrees. The length of A, B, is 9 millimeters. The triangle is is cut in half by a line, D, E, drawn from D perpendicular to line A, B, at E. A, E is 4.5 millimeters. Angle A, D, E, is 16 degrees.