
Home > GC > Chapter 5 > Lesson 5.1.3 > Problem 5-27
5-27.
Mervin and Leela are in bumper cars. They are at opposite ends of a
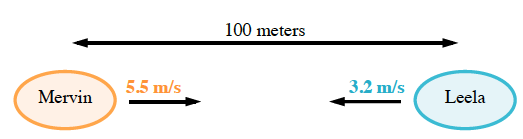
Let
Remember Mervin is starting at
So the equation for Mervin's position is
Do the same for Leela. Remember that her growth is negative and her starting position is different
Since Mervin and Leela will meet in the same position, set