
Home > MC1 > Chapter 10 > Lesson 10.2.3 > Problem 10-100
Ann and Nate's math class had a popcorn party. Each student made a container for popcorn by rolling up a piece of paper that was
Whose tube holds the most popcorn? How much more does it hold than the other tube?
This is Ann's tube. You can use the same method as Nate's tube to find the volume.
This is Nate's tube. The height of the tube is
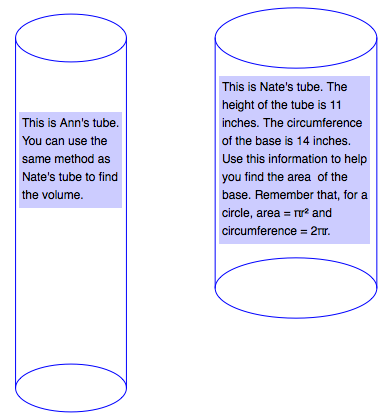
circumference
radius
area
volume = (area of base) (height)
volume
Nate's tube has a volume of
Remember to show your calculations and to figure out how much more popcorn Nate's tube holds.