CPM Homework Help : INT3S Problem 8-93

Home > INT3S > Chapter 8 > Lesson 8.3.1 > Problem 8-93

8-93.

Ahora Carlos necesita resolver $2x^{3} + 3x^{2} – 8x + 3 = 0$ , pero su calculadora aún puede crear únicamente gráficos con una ventana de visualización estándar. Él observa que el gráfico de $y = 2x^{3} + 3x^{2} – 8x + 3$ cruza el eje $x$ en $x = 1$ . ¿Cuáles son las tres soluciones a la ecuación $2x^{3} + 3x^{2} – 8x + 3 = 0$ ?

Pista:

Si $x = 1$ , entonces $x − 1 = 0$ .
Así que divide $2x^{3} + 3x^{2} − 8x + 3 = 0$ entre $x − 1$ .

Paso 1:

Paso 2:

Paso 3:

Paso 4:

Paso 5:

Paso 6:

Paso 7:

Paso 8:

Paso 9:

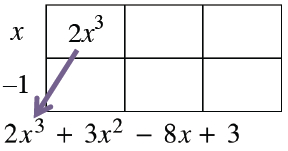
2 by 3 rectangle, labeled as follows: left edge, x, minus 1, interior top left, 2, x cubed, bottom expression: 2, x cubed, + 3, x squared, minus 8, x, + 3. An arrow points from the interior 2, x cubed to the bottom, 2, x cubed.

Label added: top edge, left, 2, x squared.

Label added: interior bottom, left, negative 2, x squared.

Label added: interior top middle, 5, x squared, with arrow, going through, interior bottom left, negative 2, x squared, ending, in the bottom expression, at 3, x squared.

Label added, top edge, middle, 5, x.

Label added, Interior bottom, middle, negative 5, x.

Label added, interior top, right, negative 3, x, with arrow, going through, interior bottom, middle, negative 5, x, ending, in the bottom expression, at negative 8, x.

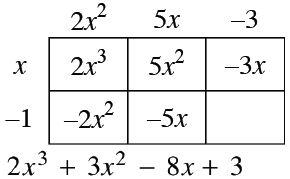
Label added, top edge, right, negative 3.

Label added, interior bottom, right, 3.

Paso 10:

Escribe la ecuación en la forma factorizada.
$\left(x − 1\right)\left(2x^{2} + 5x − 3\right) = 0$

Más Pasos:

Factoriza la expresión cuadrática y usa la propiedad del producto cero para obtener las tres soluciones.